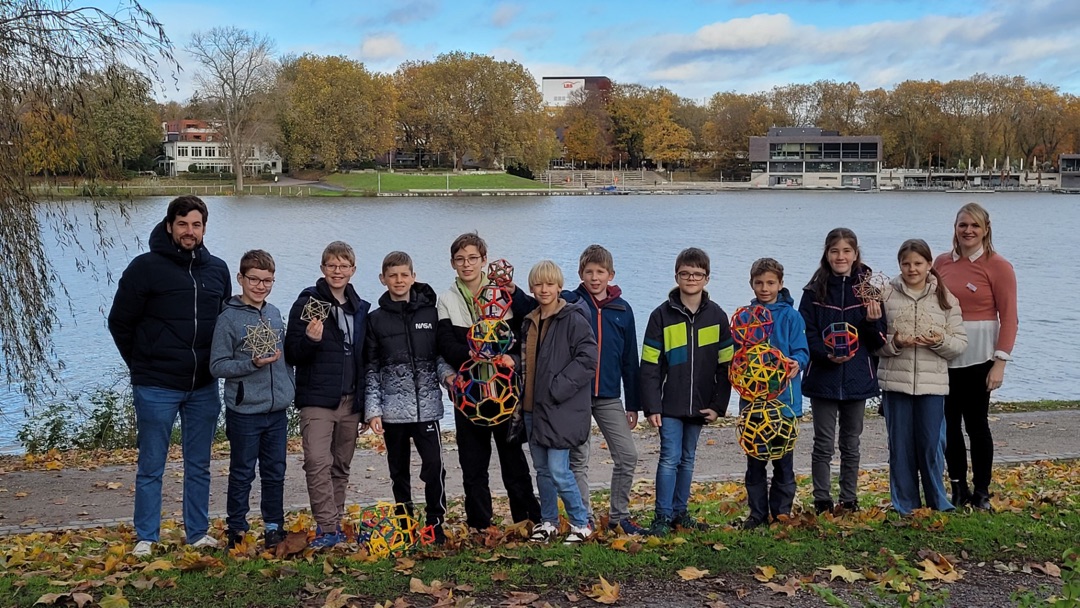
Was hat ein Fußball mit Mathe zu tun? Wie häufig muss man ein Blatt Papier falten, um ein so dickes Blatt zu erhalten, dass es von der Erde zum Mond reicht? Mit diesen und vielen anderen Fragen habe ich mich vom 9.11.2023 bis zum 11.11.2023 bei der SAMMS (Schülerakademie für Mathematik in Münster) zusammen mit 49 anderen Schülern der 6. Klassen des Regierungsbezirks Münster beschäftigt.

Aufgeregt machte ich mich am Donnerstagmorgen auf den Weg zum Aasee, um dort am Jugendgästehaus viele neue Gesichter von Schülern und Lehrern zu sehen. Zu Beginn der Akademie wurden uns die möglichen Themen vorgestellt, mit denen man sich in den nächsten Tagen beschäftigen konnte:

• Rätselreise um die Welt
• Strichcodes - Das Geheimnis der Zebrastreifen
• Alles geheim? - Macht nix! Geheimschriften entschlüsseln
• Ganz besondere Körper: Platonische sowie archimedische Körper
• Programmierung von 3D-Geometrie-Modellen für AR- und 3D-Druck-Systeme

Meine Wahl fiel auf die platonischen und archimedischen Körper.
Was auf den ersten Blick vielleicht kompliziert oder langweilig klingt, entpuppte sich als wirklich spannendes und anwendungsbezogenes Thema! So ist ein klassisches Beispiel eines archimedischen Körpers der Fußball.
Doch was macht die archimedischen und platonischen Körper aus? Um diese Frage zu beantworten, haben wir aus Erbsen und Zahnstochern den kleinsten Körper, den es gibt, gebaut: den Tetraeder (also eine Pyramide mit dreieckiger Grundfläche).

Anhand dieses Beispiels haben wir gelernt, dass ein platonischer Körper nur aus ein und denselben Flächen zusammengesetzt ist, das er immer gleich aussieht, egal wie man ihn dreht und wendet und dass an jeder Ecke gleich viele Kanten bzw. Flächen zusammenlaufen. Das Gleiche gilt auch für archimedische Körper, nur, dass sie auch aus verschiedenen Flächenarten bestehen können.
D.h. ein platonischer Körper ist immer auch ein archimedischer Körper, aber nicht umgekehrt! Das überraschende Ergebnis, das es nur fünf verschiedene platonische Körper gibt, haben wir daran wie folgt erkannt. Wenn man eine andere Art von Flächen als gleichseitige Dreiecke, Quadrate, regelmäßige Fünfecke zusammenbaut, ergibt dies eine Fläche und keinen Körper.

Als wir die Anzahl der Ecken, Kanten und Flächen aller platonischen Körper aufschrieben, erkannten wir einen Zusammenhang: den Euler‘schen Polyedersatz. Dieser besagt, dass bei jedem Polyeder die Anzahl der Ecken plus die Anzahl der Kanten minus die Anzahl der Flächen genau zwei ergibt. Auch, wenn wir viel Theorie gelernt haben, haben wir alle Dinge praktisch angewendet: So konnten wir eine riesige Sierpinski-Pyramide aus Erbsen und Zahnstochern bauen.

Auch ein Ausflug zum Planetarium in Münster gehörte zum Programm. Als krönender Abschluss hat jede Gruppe ihre Ergebnisse den Eltern, Lehrern oder anderen Interessierten bei der Abschlusspräsentation vorgestellt.

Es waren interessante und spannende zweieinhalb Tage, in denen Freundschaften entstanden sind und so mancher Ah-ha Moment passiert ist.

Ach übrigens, man muss das Blatt Papier nur 41-Mal* knicken und schon hat man die Strecke zum Mond erreicht. Probiert es mal aus 😉!

Von Leonard Wirth aus der 6c

* Nach 41mal Falten hat man 2⁴¹ Lagen Papier! Nimmt man an, dass eine Lage Papier 0,18mm dick ist, ergibt das über 395.824 km, wobei die Entfernung zum Mond in etwa 380.000 km beträgt.

Weitere Bilder: